1. Dimensions

By K. R. "Mack" Mackenzie, with review and editorial by Tom Faulhaber and the NodeWarrior crew at Certive, Inc.

Definition:

Dimensions are the building blocks on which spaces are defined and upon which constraints operate. At their most fundamental level, they provide a simple and reliable mechanism for organizing and locating points within a space that abstracts many discontinuities and inconsistencies in the space.

We define a dimension as an index set for a space. A space is defined on one or more dimensions. The cartesian product of the members of these index sets can uniquely identify every point in the defined space.

Continuous vs. Discrete Dimensions

A dimension can be continuous:

or discrete:

Continuous dimensions are uncountable and have the property that for a continuous dimension for any two elements there exists a third element such that. The set of all real numbers is an example of a continuous dimension.

Discrete dimensions have countable members. Common examples of discrete dimensions are the set of integers, the alphabet, or a set of records in a table.

There is a third kind of dimension, a composite dimension. This type of dimension contains discontinuous regions of discrete and/or continuous members. Composite dimensions are not clearly defined at present and a more detailed discussion of their properties will be left for another time.

Properties of Dimensions

Bounded and Unbounded

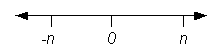
A dimension can be bounded or unbounded. It can have upper bounds or lower bounds. A dimension with both upper and lower bounds is bounded or fully bounded. A dimension with only upper or lower bounds but not both is partially bounded.

Unbounded:

Partially bounded:

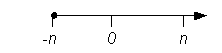
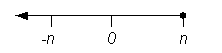
Fully bounded:

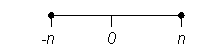
Properties of Continuous Dimensions

Examples of Bounding on Continuous Dimensions

A partially bounded continuous dimension with a lower bound:

A partially bounded continuous dimension with an upper bound:

A bounded continuous dimension:

Properties of Discrete Dimensions

Discrete dimensions can be broken into three subclasses of decreasing specificity:

á Cardinal – In a cardinal dimension, the members map directly on to a subset of the integers and the definitions of distance and order are meaningful.

á Ordinal – In an ordinal dimension, the members map directly on to a subset of the integers whose members are not guaranteed to be contiguous. This is useful for determining order but does not allow any determinations of distance. Distance is meaningless in ordinal dimensions.

á Nominal – In a nominal dimension, neither order nor distance are meaningful concepts. There is no defined relationship between the elements. This is useful for dimensions that enumerate categories (for example, sales regions).

Bounding of Discrete Dimensions

By default, all simple discrete dimensions are bounded because they are defined by enumerating the members of the set. Such dimensions are called enumerated dimensions. They are implicitly bounded. The previous example of a discrete dimension is an enumerated dimension: .

Discrete dimensions can be partially bounded or unbounded if they have a forward extrapolation or backward extrapolation function defined for them and they also have corresponding upper or lower bounds.

A forward extrapolation function is one that provides:

Correspondingly, a backward extrapolation function defines:

Therefore, a partially bounded discrete dimension with an implicit lower bound would be:

The subset of is called the concrete portion of . Likewise, the subset is the extrapolated portion of .

A partially bounded discrete dimension with an implicit upper bound would be:

A simple unbounded discrete dimension would at a minimum look like this:

This definition is only useful if the extrapolation functions carry in their definitions an internal reference to some implicit member of (typically 0 or the equivalent origin value). A more absolute definition includes at least some concrete portion. In the example:

It is much clearer what the exact value for any given must be since we can see some specific concrete members of for the extrapolation functions to operate on.

In a partially bounded or unbounded discrete dimension, it is meaningful to further bound it by defining explicit upper or lower bounds. For example:

is a fully bounded discrete dimension because of the addition of the explicit upper bound .

Mapping Continuous Dimensions to Discrete Dimensions

A continuous dimension and a discrete dimension can be considered equivalent if:

is a continuous dimension:

is a discrete dimension:

iff

and they have corresponding bounds:

A continuous dimension can be treated as an equivalent discrete dimension if it has a pair of enumerator functions defined for it:

such that:

A discrete dimension can be treated as an equivalent continuous dimension if it has an interpolation function defined for it such that: